A series circuit is a circuit that all components are connected in series with one's end connected to the other's beginning. The following circuit shows three resistors connected in series: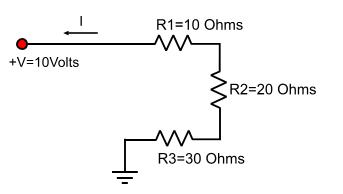

The total resistance is the mathematical sum of all resistors and it is bigger than the part with the biggest resistance.

In our previous example, the total R_TOTAL is:

Current is the same for all parts in the circuit and it is equal to I total.

Using the Ohm's law, you can calculate the total current:

This amount of current is equal for every part. This means that I_TOTAL flows through R1, R2 and R3 and it is 10Volts / 50 Ohms = 0.2 Amperes = 200 mA

The sum of the voltage drops on every part in a series circuit is equal to the applied voltage.

Every part connected to a power supply causes a voltage drop that can be measured on it's pins. This voltage drop can be calculated by the ohm's law and it is: U = R x I. In a series circuit, every resistor may have different voltage drop measured on it's pins but adding all drops of every component must have the supply voltage. So:

A parallel circuit is a circuit that all components are connected in parallel, the beginnings and the ends of all components connected together. The following circuit shows three resistors connected in parallel: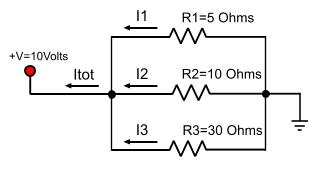

The total resistance of the circuit is calculated with the following type and it is smaller than the part with the smaller resistance:

In our example:

An exception that makes our life easier is if we have to calculate only two resistors in parallel. In this case, there is a special type that can calculate the R total and it is:

It looks more easier to calculate. If we have more than two resistors this type cannot be applied directly. It is possible to calculate the Rtotal in steps by calculating each time two resistors. In our example:

Some people do prefer this method as it is easier to calculate it 'by heart' without calculator.

The total current drawn by the source is the mathematical addition of each current that flows through every part.

where Ixxx is the current that flows in every part of the circuit. In our example, this means that:

Voltage drop is the same for every part in the circuit. Obviously, this is true as every part is connected directly to the power supply. This is very helpful to know when you have some parts like 12Volt lamps to connect to a 12Volt power supply. Connecting them in parallel will make sure that every lamp will have 12Volts on it's pins.

Rate this article!

Name   Email (shall not be published)   Website Notify me of new posts via email Write your comments below: